EHD Equations Scaling with external convection
The following blog post extends my dimensionless theory for EHD propulsion in the case of the presence of a strong external convection field.
The issue of the addition of the mean flow is a crucial aspect to consider when examining the motion of a thruster in relation to a still air volume. It is essential to understand the impact that this addition has on the generated thrust force and the power consumption of the thruster.
The velocity, denoted as \(U\), of the moving thruster is determined by the equilibrium condition \(T(U)-D(U)=0\), where \(T(U)\) is the thrust force generated by the thruster and \(D(U)\) is the drag force experienced by the vehicle.
It is important to note that analyzing the functional form of \(T(U)\) requires expensive wind tunnel testing. Hence, it is imperative to study what the dimensionless model can tell us about this dependence.
To construct suitable reference values for the dimensionless model, the gap is chosen as the main geometric scaling length, and the applied voltage is chosen as the main electrical quantity. The mean flow velocity can be scaled with a \(u_{\infty}\) term that represents the order of magnitude of such velocity.
\[\begin{cases} \hat{\nabla} \cdot \hat{E} = \dfrac{\rho_0}{\epsilon_0 \dfrac{V_a}{d^2}}\hat{\rho} \\ \hat{\nabla} \cdot \hat{\rho} \left( \hat{E} + \dfrac{u_{\infty}}{\mu_q \dfrac{V_a}{d}} \hat{u} \right) = 0\\ \hat{u} \cdot \hat{\nabla} \hat{u} = -\dfrac{P_0}{\rho u_{\infty}^2} \hat{\nabla} \hat{P} + \dfrac{\rho_0 V_a}{\rho u_{\infty}^2} \hat{\rho}_q \hat{E} + \dfrac{\nu}{ u_{\infty} d} \hat{\nabla}^2 \hat{u} \end{cases}\]hence
\[\begin{cases} \hat{\nabla} \cdot \hat{E} = \hat{\rho} \\ \hat{\nabla} \cdot \left( \hat{E} + R_v \hat{u} \right) = 0\\ \hat{u} \cdot \hat{\nabla} \hat{u} = -\hat{\nabla} \hat{P} +\left( \dfrac{1}{R_v} \dfrac{1}{\mu_q}\sqrt{\dfrac{\epsilon_0}{\rho}} \ \right)^2 \hat{\rho}_q \hat{E} + \dfrac{1}{Re_{\infty}} \hat{\nabla}^2 \hat{u} \end{cases}\]The first dimensionless number, \(R_v\), represents the ratio between the neutral gas and ion velocity and indicates the weight of the convective term in the equations. This number is significant because it helps us understand the importance of the convective term in relation to the other terms in the equations and its effect will be thoroughly explored. The second dimensionless number, \(Re_d\), represents the Reynolds number based on the convective velocity and the gap.
Upon examining the velocity ratio dimensionless number, \(R_v\), we can see that it acts as a denominator in the volumetric EHD force. This implies that the addition of a mean flow results in a reduction of the significance of this term.
This observation is intuitive since in the still case, it was the collisions between ions and neutral gas that generated the air flow. However, in the presence of a mean flow, the airflow is already present, and the effect of collisions becomes less evident in the equations as the velocity is increased.
Therefore, the addition of a mean flow has a damping effect on the volumetric EHD force, making it less significant.
The dimensionless equations are now simplified in the case of a 1D motion. The conservation of mass in the case of a 1D flow shows that this velocity is equal everywhere in the domain and it is assumed to be equal to its reference value, \(u_{\infty}\). The addition to this hypothesis yields the following drift region equations
\[\begin{cases} \dfrac{\partial}{\partial x} \hat{E} = \hat{\rho}_q \\ \dfrac{\partial}{\partial x} \hat{\rho}_q \left( \hat{E} + R_v \right) = 0 \end{cases}\]After integrating the two differential equations over the interval [0,1] and applying Peek’s boundary condition, we obtain an algebraic equation that describes the current density as a function of the dimensionless voltage and the dimensionless velocity ratio.
\[1 = \dfrac{-\left(\hat{V}^{-1}+R_v \right)^3+\sqrt{\left(\left(\hat{V}^{-1}+R_v \right)^2+2 \hat{\jmath} \right)^3}}{3\hat{\jmath}} - R_v\]The algebraic equation that describes the current density as a function of the dimensionless voltage and the dimensionless velocity ratio has a rather complex closed-form solution, which is crucial for understanding the behavior of the system since the dimensionless current is equal to the power coefficient. This solution is conveniently presented in the next figure
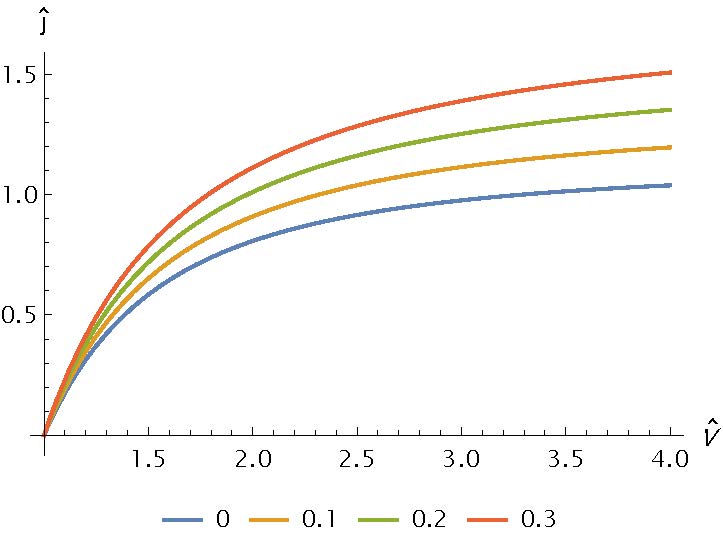
Upon examining the curves, it becomes apparent that the dimensionless current increases significantly as the effect of the convective term is amplified. This increase can be attributed to the fact that the presence of a mean flow will extract more ions from the ionization region, leading to a higher current consumption. The addition of a mean flow alters the ion flow behavior, resulting in more ions being expelled from the thruster’s ionization region. As a result, a higher current is required to maintain the desired thrust force. This effect is more pronounced at higher values of the dimensionless velocity ratio, indicating that the velocity of the thruster relative to the still air volume has a significant impact on its power consumption.
The thrust coefficient was defined as the volumetric integral of the thrust density term. In a 1D formulation, this coefficient is equivalent to a surface thrust density and the volumetric integral reduces to a line integral.
\[C_T = \int_0^1 \hat{\rho}_q \hat{E} \ \rm{d}\hat{x} = \hat{\jmath} \int_0^1 \dfrac{\hat{E}}{\hat{E} + R_v} \ \rm{d}\hat{x}\]This integral admits a, rather complex, closed-form solution, which is not reported for brevity.
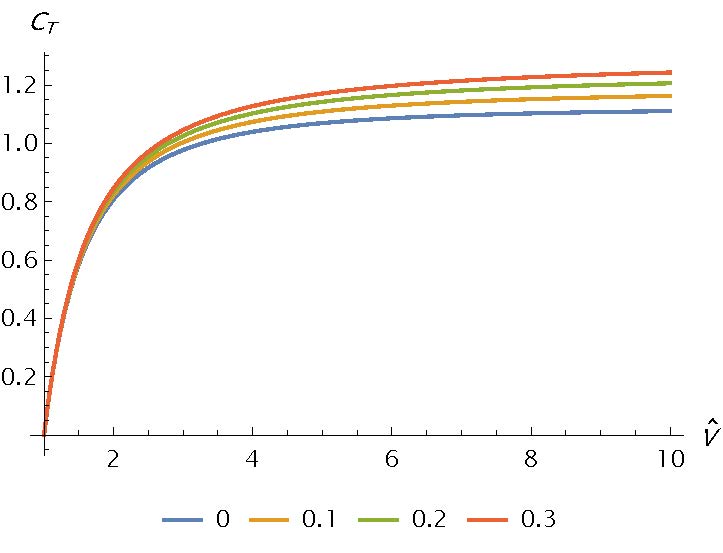
The figure above reports the thrust coefficient functional dependence on the dimensionless voltage for different values of the convective term, \(R_v\). The behavior of this value may be similar to the case of the thruster in the still air as it exhibits similar low and high voltage limits. Increasing the convective term increases the thrust coefficient but this increase is smaller if compared to the power coefficient; moreover, the actual thruster suffers from the addition of aerodynamic drag which increases as the mean flow velocity is increased. The thrust-to-power coefficient is defined as the ratio of the thrust coefficient and the power coefficient. The power coefficient asymptotic values increase significantly, being equal to the current density coefficient, as the mean flow value increases whereas the thrust coefficient undergoes a less significant increase.
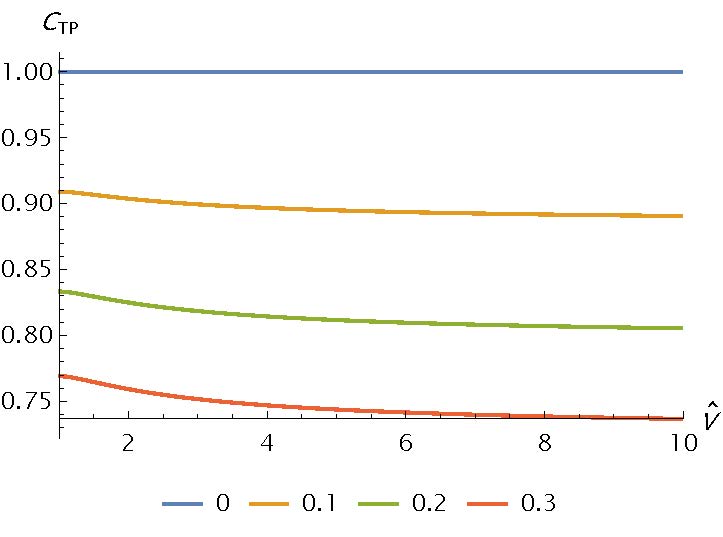
The figure shows the behavior of the thrust-to-power coefficient as a function of the dimensionless voltage and for different convective term values. It is possible to conclude that the 1D model predicts a substantial loss in the thrust to power. This is also worsened by the presence of aerodynamic drag which reduces the generated thrust.
These results are of critical importance for any future application of this technology. A reduction of the total thrust to power means that, for a given power requirement, the thruster will be able to generate less thrust as the velocity increases greatly limiting the speed of ionic thrusters. —
It is useful to note that the exact same results are obtained by studying a similar problem, i.e. the one of a thruster in variable atmospheric conditions. In this case, however, the scaling to be followed is the one indicated by my article
2023
-
 Scaling relations for the geometry of wire-to-airfoil atmospheric ionic thrustersJournal of Electrostatics, 2023
Scaling relations for the geometry of wire-to-airfoil atmospheric ionic thrustersJournal of Electrostatics, 2023
In this case, however,
\[R_v = \dfrac{1}{\mu_q}\sqrt{\dfrac{\epsilon_0}{\rho}}\]An increase in \(R_v\) can be obtained by a decrease in the air density or the ion mobility. This will produce the same effects described above.